[BOJ] 백준 15650 N과M (2) js nodejs - 간결과 효율 부족

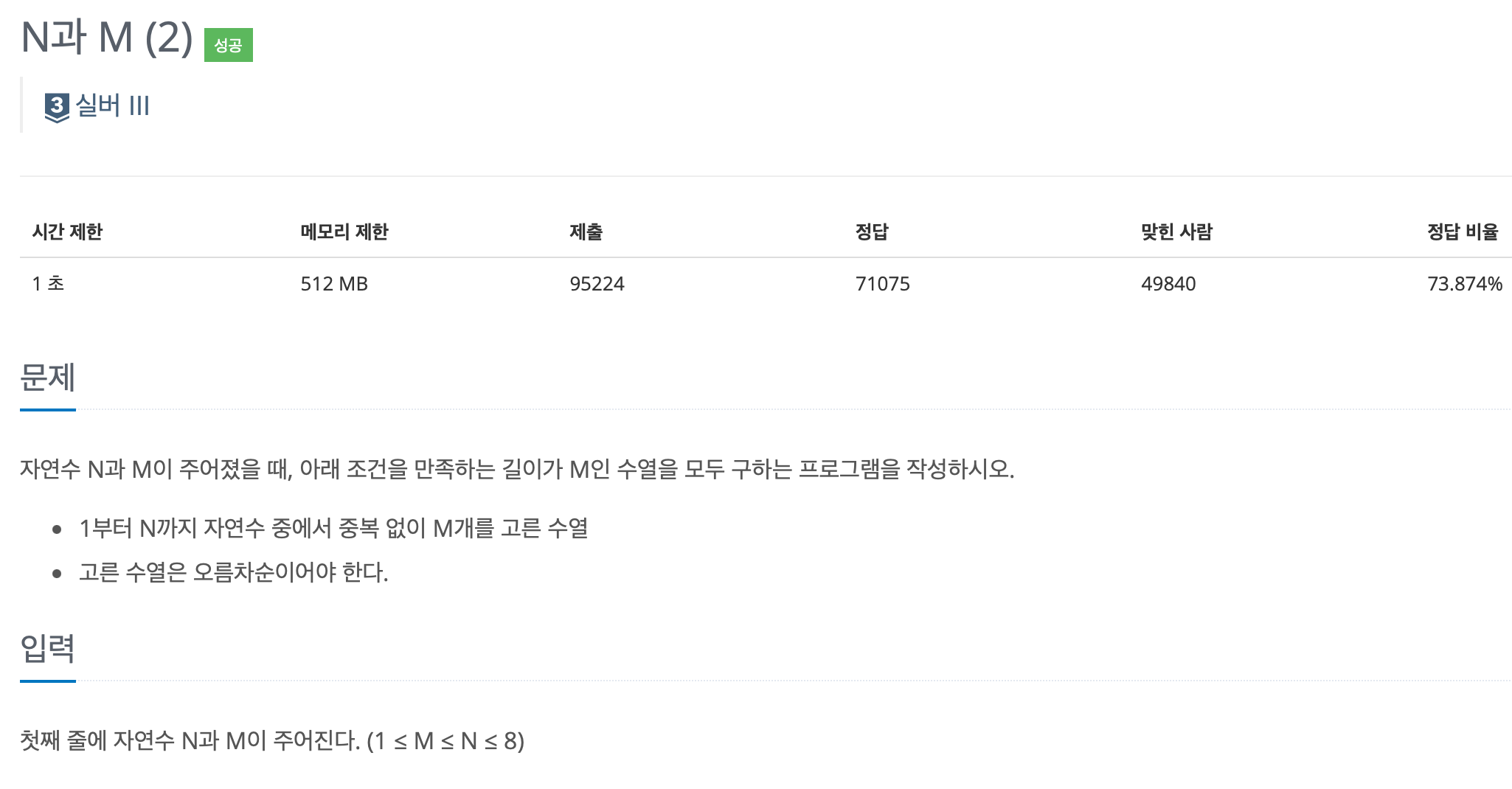
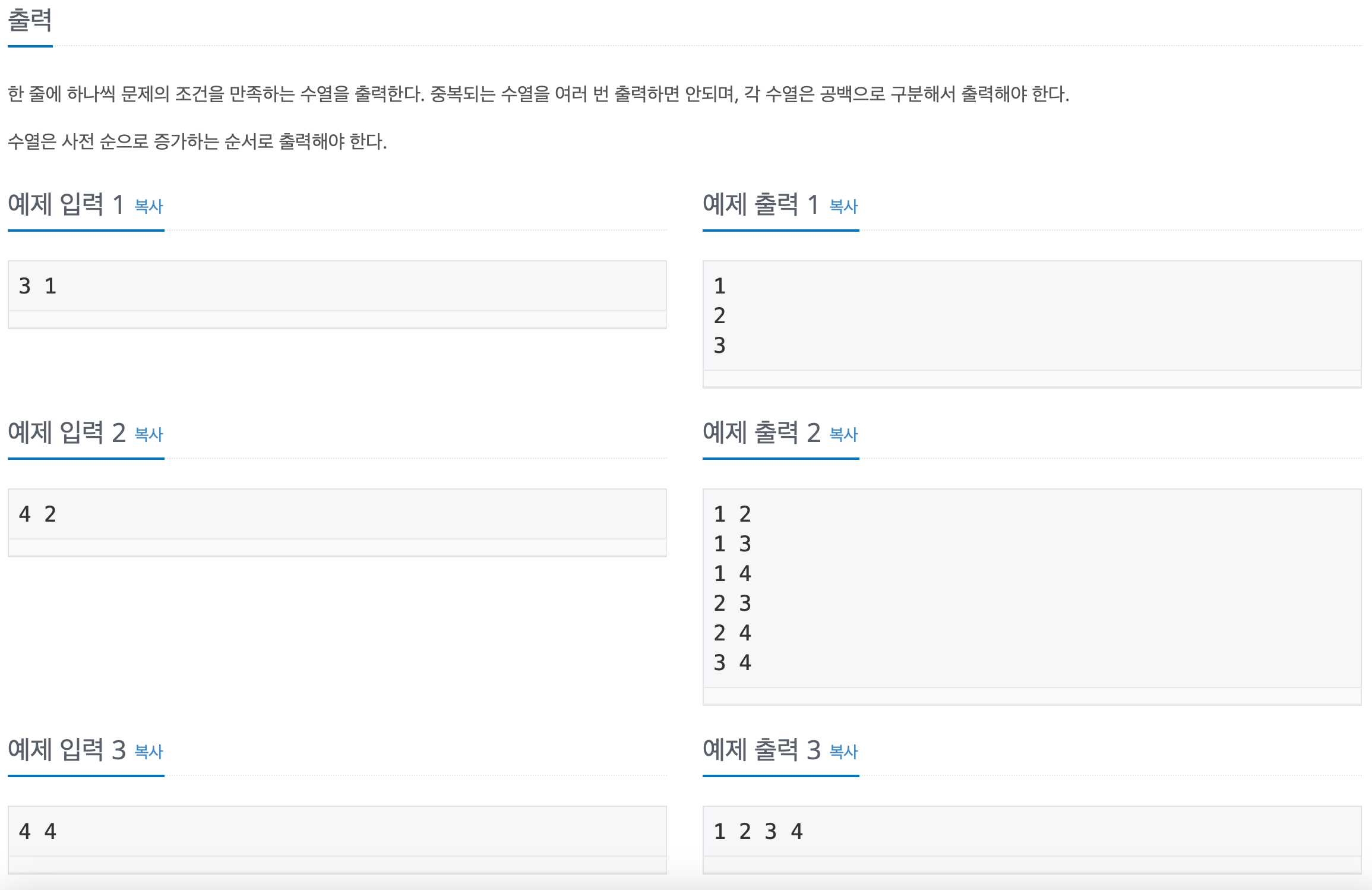
백준 15650 문제는 "1부터 N까지 자연수 중에서 중복 없이 M개를 고른 뒤 오름차순으로 출력하는" 전형적인 조합 문제입니다. 처음에는 단순히 res.includes()로 중복을 체크하고, 오름차순인지 매번 검사하는 식으로 코드를 작성했습니다. 이 방식도 입력이 아주 크지 않다면 통과하긴 하지만, 조금 더 효율적으로 작성할 수 있는 방법이 있더군요.

이 글에서는 제가 처음에 썼던 코드와, 강사님의 예제 코드를 비교해보겠습니다. 마지막에는 비슷한 문제를 만났을 때 어떻게 접근하면 좋을지, 그리고 추가 팁을 간단히 정리해봤습니다.

---

처음에 작성했던 코드

let fs = require("fs");
let read = fs.readFileSync("/dev/stdin").toString().trim();
let base = read.split(" ").map(Number);

let res = [];

const dfs = (max) => {
  if (res.length === base[1]) {
    let sortedArr = res.slice().sort((a, b) => a - b).join(" ");
    if (sortedArr === res.join(" ")) {
      console.log(res.join(" "));
    }
    return;
  }

  for (let i = 1; i <= max; i++) {
    if (!res.includes(i)) {
      res.push(i);
      dfs(max);
      res.pop();
    }
  }
};

dfs(base[0]);

이 코드는 모든 순열을 만든 뒤, 그중에서 “오름차순인 경우”만 출력합니다. 어떻게든 정답은 맞출 수 있지만, 몇 가지 문제가 존재합니다.

동작 방식

• dfs(max) 안에서 res 배열에 숫자를 중복 없이 넣었다가(if (!res.includes(i))) res.length가 M에 도달하면 오름차순 여부를 확인합니다.
• 오름차순인지 판단하기 위해 매번 res.slice().sort()로 정렬한 값과 res.join(" ")을 비교합니다.

문제점

1. 불필요한 연산이 많음
   • 실제로는 오름차순 조합만 구하면 되는데, 순열 전체를 만들면서 매번 정렬하고 비교합니다.
2. N과 M이 커질수록 비효율적
   • 순열을 전부 생성하니, 최대 (P(N, M) = \frac{N!}{(N-M)!}) 번의 탐색이 이뤄집니다. 오름차순 조합 개수((\binom{N}{M}))와 비교하면 훨씬 큰 수치입니다.

---

강사님 예제 코드

아래 코드는 강사님이 예시로 보여주신 코드입니다. 오름차순을 애초부터 직접 만들어내기 때문에, 불필요한 필터링 과정을 건너뛸 수 있습니다.

let fs = require('fs');
let input = fs.readFileSync('/dev/stdin').toString().split(" ");
let N = parseInt(input[0]);
let M = parseInt(input[1]);

let res = [];

function dfs(start) {
  if (res.length === M) {
    console.log(res.join(" "));
    return;
  }
  for (let i = start; i <= N; i++) {
    res.push(i);
    dfs(i + 1);
    res.pop();
  }
}

dfs(1);

내 코드에 비해 나은 점

1. 조합을 직접 생성
   • dfs(start)에서 start 이상의 숫자만 선택하도록 함으로써, 오름차순이 보장됩니다.
2. 정렬 과정이 필요 없음
   • 결과가 이미 오름차순으로 만들어지므로, 매번 sort()해서 비교할 필요가 없습니다.
3. 시간 복잡도 개선
   • 오름차순 조합만 탐색하므로, 전체 탐색 횟수는 n choose m 정도로 제한됩니다.

---

앞으로는?

앞으로 비슷한 문제를 마주친다면 어떻게 해야 할까요?

1. 조합 문제는 “start” 인자를 활용
   • 중복 없이 오름차순으로 뽑아야 할 때는 “다음에 선택할 수 있는 수”를 start라는 매개변수로 관리하면, 자연스럽게 오름차순을 유지하면서 중복을 막을 수 있습니다.
2. 순열인지 조합인지 먼저 구분
   • 순열 문제라면 모든 경우를 고려하되, 방문 여부(visited)나 중복 검사를 적절히 해주면 됩니다.
   • 조합 문제라면, 위처럼 start만 늘려가며 탐색하는 방식을 쓰는 편이 보통 더 깔끔합니다.
3. 정렬 검사는 최후의 수단
   • 결과를 한 번에 다 모아서 정렬 후 출력하는 대신, 생성 과정에서 바로 오름차순을 유지하면 불필요한 작업을 줄일 수 있습니다.

---

추가 팁을 AI에게 물어봤습니다.

• 백트래킹 함수 설계
  • dfs(depth, start), dfs(start, chosen) 등으로 매개변수를 조금 더 세부적으로 두면, 코드를 작성할 때 로직이 직관적으로 드러납니다.
• 출력 방식을 간소화
  • 한 번에 모아서 출력하기보다는, 조합 하나 완성 시 바로 console.log를 호출하는 편이 보통 간단합니다.
• 조건이 복잡해질 경우
  • 예를 들어, “같은 수는 최대 두 번까지 사용 가능” 같은 추가 조건이 붙으면, 조합/순열과 같은 기본 틀에 조건만 살짝 얹어가면서 구현하면 됩니다.

---

코멘트

통과 해서 싱글벙글 하면서 풀이 강의를 들었는데, 코드가 참 다르더군요...

처음 코드도 기능 자체는 동작하지만, 조합을 구하는 문제에서 순열을 전부 생성하고 그중 오름차순만 골라내는 방식은 다소 비효율적입니다. 강사님 코드처럼 애초에 오름차순 조합만 뽑는 구조를 갖추면, 훨씬 적은 연산으로 문제를 풀 수 있습니다.

비슷한 문제를 만났을 때는 “조합인지 순열인지”, 그리고 “오름차순이 필요한지”를 먼저 확인한 뒤, 가능한 한 생성 과정에서 조건을 만족하도록 구현해보시길 권합니다. 그렇게 하면 불필요한 검사나 중복 연산을 크게 줄일 수 있을 것입니다.